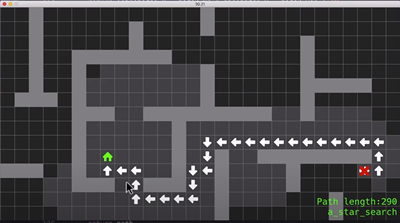
What is Dijkstras shortest path algorithm?
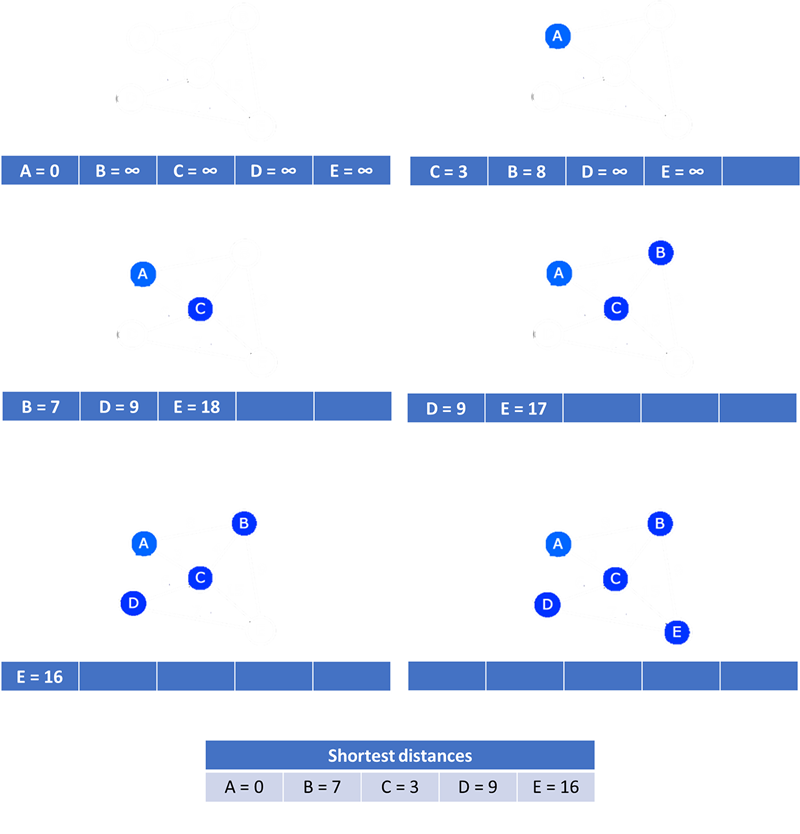
Dijkstra's shortest path algorithm is an optimization algorithm designed to find the shortest path between one node and every other node in a weighted graph.
It uses a priority queue containing the nodes of the graph with the priority being the distance to the node. To begin it is 0 from the first node to itself and an unknown distance to other nodes represented by infinity.
At each node we update the distance to its neighbours, taking account of any distance already travelled to this node. The next node is the node at the head of the priority queue i.e. the one that currently has the lowest
distance from the original node.
Uses of Dijkstra’s shortest path
Dijkstra's shortest path algorithm is useful for finding the shortest distance between 2 places on a map and routing protocols for networks.
A* algorithms (Extension for AQA)
Dijkstra's algorithm finds the best path to all locations where as an A* algorithm is trying to find the fastest route to a specific target node. Dijkstra's algorithm tracks one cost which is the value on vertices connecting
nodes but A* algorithms also consider the approximate distance from each node to the target node. The total cost of a node is the cost from the source node to the current node plus the approximate cost from the current node to
the target node.
The total cost from the current node to the target node is not known so it must be approximated using a heuristic method. A heuristic method is a method that is good enough while not perfect. There are many ways to
approximate the distance to the target but the method should never overestimate the distance i.e. the real distance should be equal to or greater than that predicted by the heuristic.
A* algorithms are commonly used in GPS systems tracking fastest routes and to allow game sprites to navigate a map.