Graph traversal algorithms
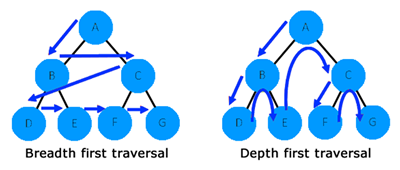
Graph traversal algorithms are designed to visit every node in a graph. There are two types of graph traversal algorithms:
- Depth first search
- Breadth
first search
Depth first traversal
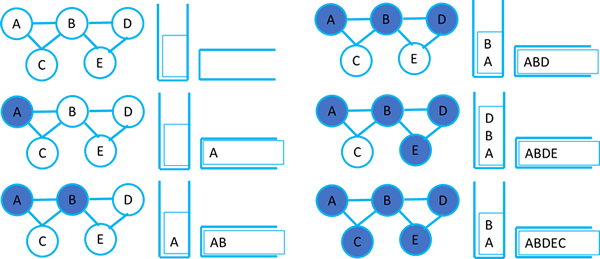
A depth first traversal goes as far down one route as it can before backtracking and taking the next route. It uses a stack and a list of visited nodes to keep track of where it has been so it can backtrack.

We start with an empty list of visited nodes and an empty stack.
We visit node A. Node A is added to the visited list.
We visit node A's first neighbour node B. Node B is added to the visited list and Node A is
pushed to the stack so we know where we have been.
We visit node B's first neighbour node D. Node D is added to the visited list and Node B is pushed to the stack so we know where we have been.
Node D has one neighbour
we have not visited so we visit Node E. Node E is added to the visited list and Node D is pushed to the stack.
There are no new nodes to visit so we pop Node D off the stack and return to it. There are no new nodes to visit
so we pop Node B off the stack. Node B has an unvisited neighbour so we go to Node C. Node C is added to the visited list and Node B is pushed to the stack so we know where we have been.
There are no new neighbours to visit
from Node C so we pop Node B off the stack and return to it. It also has no unvisited neighbours so we pop Node A off the stack and return there. Node A has no unvisted neighbours so we pop it from the stack and our depth
first traversal is complete.
Applications of depth first traversal
Depth first traversal is useful in maze solving algorithms and scheduling tasks where some tasks have to be completed before the next task can start.
Breadth first traversal
A breadth first traversal visits all the neighbours of the current node before doing this for each node at the same level i.e. the same distance away from the first node. It uses a queue of nodes to visit and an array of
visited nodes.

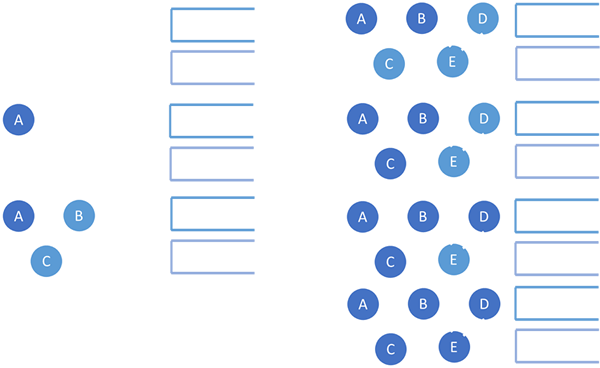
We start with an empty ueue and empty visited list.
We visit the first node, Node A. Node A is added to the visited list and its neighbours Node B and Node C are placed into the queue.
Node B is popped from the front
of the queue and visited. Node B is added to the visited list and its neighbours that are not already in the queue are added to the queue so Nodes D and E.
Node C is popped from the queue. Node C is added to the visited
list.
There are no unqueued and unvisited neighbours so Node D is popped off the stack and visited. Node D is added to the visited list.
There are no unqueued and unvisited neighbours so Node E is popped off the stack
and visited. Node E is added to the visited list. The ueue is empty and so our traversal is complete.
Applications of breadth first traversal
Breadth first traversal is useful for shortest path algorithms used in GPS devices and mapping vast webs of social media connections.