Computer systems: Boolean algebra

Boolean algebra can be used to simplify complex boolean expressions. This is helpful in designing efficient logic circuits.

Boolean identities

The following 9 boolean identities can be worked out by thinking about them. We are considering what the result of putting an unknown variabe through a series of different tests.

An AND gate must have both inputs as 1. So when we and our mystery value X with a 0 we know the result must be 0 as one input is definitely not 0.

If we and X with 1 then if X is 1 the output is 1 and if X is 0 the output is 0, therefore the output is the same as whatever X is.

If we and X with itself then if X is 1 the output is 1 and if X is 0 the output is 0, therefore the output is the same as whatever X is.

If we and X with not X then we will have a 1 and a 0 and the output will be 0.

An OR gate will output 1 if either input is 1, so if we or X and 0 then if X is 1 the output is 1 and if X is 0 the output is zero, therefore the output is the same as X.

If we or X and 1, there is definitely at least one 1 so the output is 1.

If we or X with itself then if X is 1 the output is 1 and if X is 0 the output is 0, therefore the output is the same as whatever X is.

If we or X with not X then we will have a 1 and a 0 and the output will be 1.

Not X will be the opposite of X and so not(not X) is simply X.

De Morgan's laws

De Morgan's first law

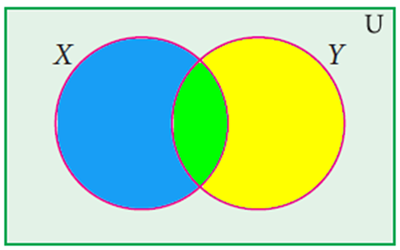
De Morgan's first law says that not(A or B) is the same as not A and not B and is written as A + B = A.B

If you examine the Venn diagram above, X or Y is anywhere inside the area covered by the two combined circles, so not(X or Y) is the light green area outside of this. If it has to be in the area outside the yellow circle and the area outside the blue circle this describes the same light green area.

De Morgan's second law

De Morgan's second law says that not(A and B) is the same as not A or not B and is written as A.B = A + B

If you examine the Venn diagram above, X and Y is the bright green area in the center, so not(X and Y) is everything outside of this. If something is not X or not Y it can also be anywhere except in the bright green section.

Commutative rules

These allow us to rearrange equations. The two rules are:

X.Y = Y.X

X + Y = Y + X

You can see in the venn diagram above these cover the same area.

Absorption rules

The absorption rules are:

X + (X.Y) = X

If you look at the venn diagram X.Y is the bright green area entirely contained inside X.

X.(X + Y) = X

If a value is in X and in X or Y it can only be in the part of X or Y that is X.

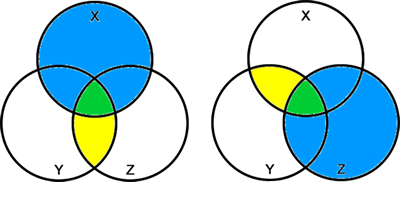
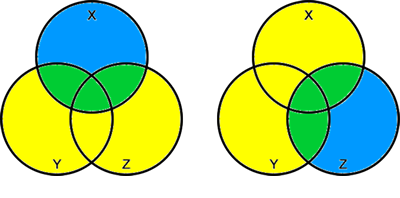
Associative rules

The associative rules are:

X.(Y.Z) = (X.Y).Z

As you can see above, regardless of whether we combine X and Y and then and that result with Z or combine Y and Z and and that result with X the same small green area is defined.

X + (Y + Z) = (X + Y) + Z

Similarly whether we look at the area covered by X or Y and or that result with Z or look at the area reoresented by Y or Z and or that with X we still define the entire area of the three combined circles.

Distributive rules

The distirbutive rules are:

X.(Y + Z) = X.Y + X.Z

(X + Y).(W + Z) = X.W + X.Z + Y.W + Y.Z

Simplifying boolean expressions

When simplifying boolean expressions you should make one change on each line and specify what rule you are relying on. Each correct application will score a mark even if you go wrong before the final answer.

Let's simplify (A+B).(B+C.(D+D))

= (A+B).(B+C.1) (X+X=1)

= (A+B).(B+C) (X.1=X)

= A.B + A.C + B.B + B.C (Distributive rule)

= A.B + A.C + B + B.C (X.X=X)

= A.B + A.C + B (Absorption rule)

= A.C + B + A.B (Commutative rule)

= A.C + B (Absorption rule)

Knowledge check

Questions:

Correct:

Question text