Backus-Naur form
The Backus-Naur form is an example of a meta language. Regular expressions can be used to define fairly simple sets. While some parts of languages such as valid identifiers could be described by regular expressions, others
like nested statements would be far more challenging. Meta languages get around this problem.
The Backus-Naur form is made up of a list of statements in the form:
something ::= something else
Where ::= means is defined by
::= is a meta symbol
Eg. <decimal> ::= .
<digit> ::= 0|1|2|3|4|5|6|7|8|9
<pound> ::= £
<price> ::= <pound><digit><decimal><digit><digit>
Values in angle brackets are known as meta-components
Each individual rule is known as a production
Backus-Naur form and recursion
A definition can refer to itself meaning it can be applied recursively. As with standard recursion there needs to be at least one case in which a definition does not call itself.
<digit> ::= 0|1|2|3|4|5|6|7|8|9
<natural_number> ::= <digit>|<digit><natural_number>
This recursive definition accounts for a number of any number of digits.
Consider 1374.
4 is a <digit> and therefore also a
<natural_number>
74 is <digit>< natural_ number> and therefore also a <natural_ number>
374 is <digit>< natural_ number> and therefore also a <natural_ number>
1374 is <digit>< natural_ number> and therefore also a <natural_ number>
Example extended
Let’s carry on with our example.
<decimal> ::= .
<digit> ::= 0|1|2|3|4|5|6|7|8|9
<pound> ::= £
<number> ::= <digit>|<digit><number>
<pence> ::=
<digit><digit>
<price> ::= <pound><number><decimal><pence>
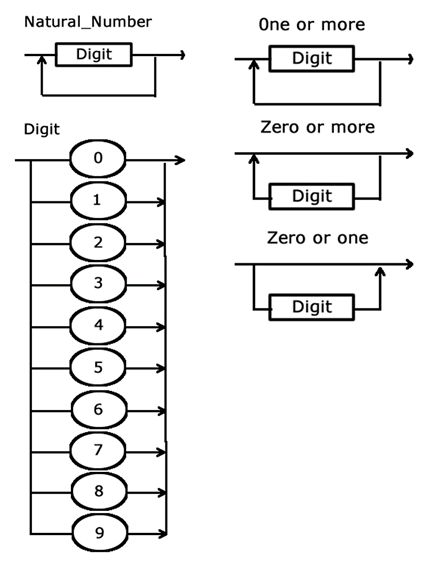
Syntax diagrams
Syntax diagrams are a diagrammatic way to represent the Backus-Naur form. An oval represents a terminal element, meaning one that cannot be further defined. A rectangle is a non-terminal element, meaning it can be further defined.
A loop can be created for optional and repeated elements.