Sets

A set is an unordered collection of values in which each value occurs at most once. A basic set can be can be defined by listing all of its members between curly braces e.g. A = {1,2,3,4,5}. A set can also be defined using set notation e.g. A = {x | x ∈ ℕ ∧ x ⋝ 1 }

| means such that
x ∈ ℕ means that x is a member of the set ℕ consisting of the natural numbers, i.e. {0, 1, 2, 3, 4, … }
The symbol ∧ means AND
The term ∧ x > = 1 means AND x is greater than or equal to 1.

An empty set can be defined as A = { } or as A = ∅

The elements of a set are also referred to as members of the set.

Compact sets

Below you can see a compact representation of a set.
{0ⁿ1ⁿ | n ⋝ 1} = {01, 0011, 000111, 00001111, … }
This set contains all strings with an equal number of 0s and 1s and where all the zeros come before all the ones.

Common sets

Finite/infinite sets

A finite set is one whose elements can be counted off by natural numbers up to a particular number e.g. 1st element, 2nd element, …, 20th (and final) element.

An infinite set goes on forever approaching infinity and or negative infinity. The set of natural numbers, ℕ and the set of real numbers, ℝ are examples of infinite sets.

A set is countably infinite if it is infinite but we could specify a certain value in the set and it would take a finite amount of time to reach that value. This is true of the sets of integers ℤ and natural numbers ℕ. It is not true of real numbers ℝ.

Cardinality of finite sets

The cardinality of a finite set is the number of elements in that set.
If A = {1,3,5} then |A| = 3

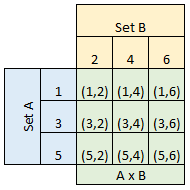
Cartesian product of sets

The cartesian product of two sets is the set of all ordered pairs (a,b) where a is a member of set A and b is a member of set B.
A x B = {(a,b) | a ∈ A ^ b ∈ B}
If A = {1,3,5} and B = {2,4,6} then:
A x B = {(1,2),(1,4),(1,6),(3,2),(3,4),(3,6),(5,2),(5,4),(5,6)}

Subsets

A proper subset is where a subset is comprised entirely of elements of another set but where there is at least one element in the original set not included in this set
e.g. {0, 1 , 2 } ⊂ ℕ
If the term used is just subset this means the subset can contain all the elements of the other set e.g. {0, 1, 2, 3 } ⊆ {0, 1, 2, 3 }

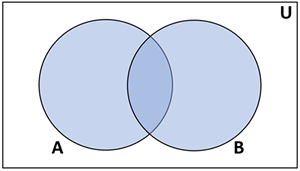
Set operations - union

The union of two sets is all the members of both sets i.e. A or B. It is all the area shaded blue below. Remember that a set only contains each value once so:
If A = {1,3,5} and B = {4,5,6} A ∪ B = {1,3,4,5,6}

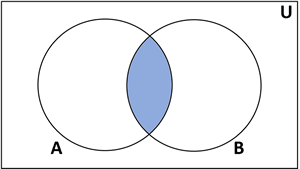
Set operations - intersection

The intersection of two sets is all the values common to both sets i.e. A and B.
If A = {1,3,5} and B = {4,5,6} A ∩ B = {5}

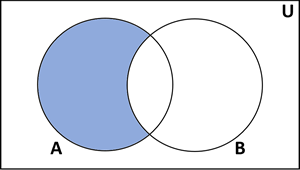
Set operations - difference

The difference of two sets is all the values of set A that are not also in set B i.e. A and not B
If A = {1,3,5} and B = {4,5,6} A \ B = {1,3}

Knowledge check

Questions:

Correct:

Question text