Bubble sort
A bubble sort makes pairwise comparisons of data in a list swapping them if out of order. When all pairwise checks have been made for an entire list, we are said to have made
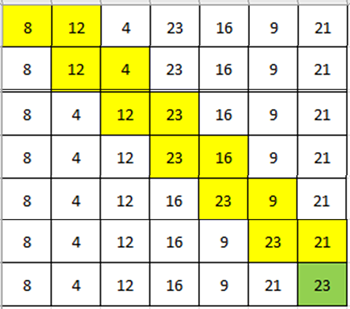
one pass of the data. After each pass the largest number will have bubbled along to the end, hence the name bubble sort. A single pass of the list [8,12,4,23,16,9,21] is shown
below. First we compare 8 and 12. They are in order so we move to the next pair. 12 and 4 are in the wrong order so we swap them and move on to the next comparison. 12 and 23
are in the right order so we move on to the next comparison. 23 and 16 need to be swapped before we compare 23 and 9 which also need to be swapped. Our final comparison this pass
is to compare 23 and 21 which also need to be swapped. At this point one pass is complete and we know that at least one item, the last one, will be in the right order. It is not,
however, the end of the bubble sort.
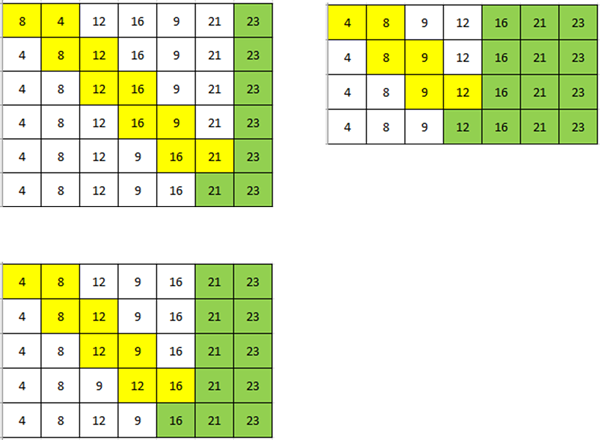
Now the process begins again with another pass of the data though we can stop one place sooner. If a full pass of the data is made and no swaps are made, then the data is fully
in order. Below you can see the 2nd, 3rd and 4th passes needed to fully sort this data.
You don't need to be able to reproduce the pseudocode for the bubble sort but you might be asked to identify it or fill in some key missing details from it.

Insertion sort
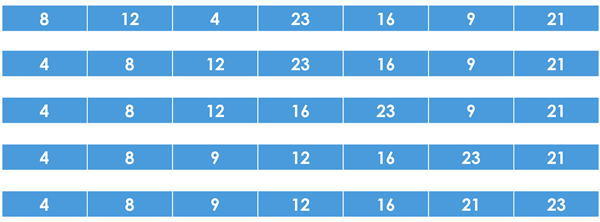
The insertion sort takes each item from left to right in the array and moves it left until it is in the correct place. First we look at the 12. It is greater than 8 so no movement.
Now we look at the 4. It is smaller than 12 so moves left. It is also smaller than 8 so keeps moving left. Now we check the 4th value 23. It is bigger than the number to its left so no
change is needed. The 16 is smaller than 23 so moves left. It is bigger than 12 so this is where it stays. The 9 moves left past the 23, then the 16 then the 12. Finally the 21 moves
one place left.
You don't need to be able to reproduce the pseudocode for the insertion sort either but you might be asked to identify it or fill in some key missing details from it.