Binary

About binary

Binary is base 2. It is a counting system where there are only 2 possible digits - 1 and 0. Our normal system is called decimal or denary. It is a base 10 counting system because there are 10 possible digits that can go in each column. The digits from 0 to 9. If we look at our base 10 system we are used to the next column over from our 1s column is the 10s column. This is because it is one bigger than we can represent in a single column. If we look to binary, we can only represent 0 or 1 1s and so the next column is the number of twos we have. Now if we were to write 11 we would be saying we have 1x2 and 1x1 or 3. The next column heading is 4. This pattern continues with the column headings doubling as we move left. You need to deal with numbers up to 8 bits in binary.

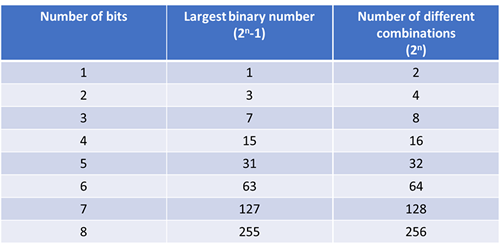
Largest number with n bits

The largest number we can make with n bits where n is the number of bits we use can be found by the formula (2^n)-1 where n is the number of bits used. This is always one less than the number of different combinations that can be made with n bits because one combination it males is 0.

Converting binary to decimal

For our example let's convert the binary number 01001011 to it's decimal equivalent.

The first step is to draw out a table and fill it in with the column headings for binary. Remember, the column headings in binary start at 1 on the right and double as you move left like below.

Then it's just a matter of adding up the column headings of the columns that have a 1 in them.

128	64	32	16	8	4	2	1
0	1	0	0	1	0	1	1

64 + 8 + 2 + 1 = 75

Test yourself

128	64	32	16	8	4	2	1
0	0	0	0	0	0	0	0

Click the button to generate a binary number to convert

The decimal equivalent is:

Decimal to binary example

For our example let's convert the decimal number 113 to it's binary equivalent.

The first step is to draw out a table and fill it in with the column headings for binary. Remember, the column headings in binary start at 1 on the right and double as you move left like below.

128	64	32	16	8	4	2	1
0	1

We start on the left. If the column heading is bigger than our number we put a 0 in that column and carry on.

If the column heading is equal to or smaller than our number we put a 1 in it. Then subtract the column heading from our number such as in this case 113 - 64 = 49

128	64	32	16	8	4	2	1
0	1	1

And we carry on following those same two rules until we have a total of 0, then any remaining columns are 0s

So to continue our example 49 - 32 = 17

128	64	32	16	8	4	2	1
0	1	1	1

17-16 = 1

128	64	32	16	8	4	2	1
0	1	1	1	0	0	0	1

1 - 1 = 0

So 113 in binary is 01110001

Test yourself

Make sure to include leading zeros. if you start on the left then the cursor will automatcally move to the next box after you type a 1 or 0

Click the button to get a number to convert

128	64	32	16	8	4	2	1

<< Previous: Units Next: Hexadecimal >>